Online Statistics Tutor: Analyzing Nominal and Ordinal Data
While nominal (categorical) and ordinal (rank order) data can't be used in standard introductory analyses, like the T or F-tests, there still is a number of options when working with these kinds of data. In this post I will point out a few of these, specifically,
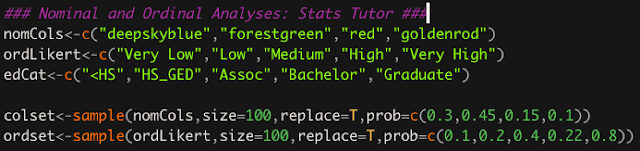
The output from sampling from the set of 4 colors and 5 items in a likert scale are saved as "colset" and "ordset". The size argument in the sample function means that this output will be 100 elements long. To produce a table of counts for these data you use the table function, as shown below.
The first table that shows the counts by colors and a likert scale is often called "cross-tabs" because it is a two dimensional table. If you want R to produce a two-dimensional table, you need only provide the data for each variable separated by a comma.
The test statistic comes from summing the deviations of the observed data has from expected values which represent the null hypothesis that there is no association. The computation for the expected cell values is represented by
The actual test statistic is computed by
I won't be taking you through the manual computations, rather I will show you how to calculate this in R using an example. This data comes from R base datasets package and contains categorical information regarding passengers aboard the ill-fated Titanic. It is a 4 dimensional table so I will demonstrate how I got this data. It can be confusing if you are not used to handling arrays.
The specific dataset I want is a 2x2 table of adult women who survived or did not, and their class.
Because I want the second element of the second and third dimensions of the array, I subset by those two and provide leave the others blank so I can see all the levels of the first and fourth dimensions. The bottom of this graphic shows the cross-tabs I will be using for this test.
I am going to test whether there was an association between the number of those that survived and passenger class for adult women. The following code will execute this test.
As you can see, the function to carry out this test is chisq.test. The p-value here is very small (p < 0.05) so I reject the null hypothesis and have sufficient evidence to claim there is an association between survival and passenger class for adult women aboard the Titanic.
The association is estimated by comparing the diagonal elements of the ordinal levels to the off-diagonal elements. While I won't get into the details, I will illustrate this concept with tables that produce perfect positive and negative associations.
The first table called "perfPos" shows a table that features 5 levels of ordinal information for each variable, where counts only appear in the diagonal elements and none in the off-diagonal ones. This is saying that as the level of one variable increases, so does the other. Conversely, the "perfNeg" table shows that as the level of one increases, the other decreases. These two tables have a gamma statistics of 1 and -1, respectively.
To make the application of this test more obvious, I created a fictitious table where one axis is education with ordinal categories and the other contains likert scale responses. Let's say that I am a public health official and I want to make an association with education and thoughts regarding immunizations. This survey has a number of questions, the first being one that asks about the respondents' level of education and the other is a question that asks "Please indicate how important you feel that immunizations are to your health and the health of your home town." After administering this survey to people in my area, I want to analyze those results in order to prove that association. The observed results provide the following cross-tabs.
The rows are the education levels and columns the responses to the question regarding immunizations. Without reading ahead, what kind of association do you see in this data based off of what you saw in the behavior of the perfect associations? Can you see a greater emphasis on the diagonal elements of the table?
The function for this gamma statistic can be found in two R packages, though I am sure there are more out there. The first being "DescTools" and the other being "vcdExtra". I like "vcdExtra" a bit more because it provides a confidence interval for the estimate.
The test statistic provides evidence for the association between education and sentiments regarding the importance of immunizations to public health.
That's a wrap for this post. Please let me know if you have any further questions, thoughts, or ideas in the comments. Lastly, feel free to ask me any specific questions at this site. Be aware that there is a nominal $1.50 fee to submit questions. That is because it takes time and effort to respond to your questions. Though, please ask questions about this specific post in the comments.
- Producing table of counts of cross-tabs.
- Chi-square test of association.
- Kruskall's Gamma: A correlation coefficient for ordinal data.
- I will provide code on how to perform each in R
The output from sampling from the set of 4 colors and 5 items in a likert scale are saved as "colset" and "ordset". The size argument in the sample function means that this output will be 100 elements long. To produce a table of counts for these data you use the table function, as shown below.
The first table that shows the counts by colors and a likert scale is often called "cross-tabs" because it is a two dimensional table. If you want R to produce a two-dimensional table, you need only provide the data for each variable separated by a comma.
Chi-Square Test of Association
One standard exploratory test of association is the chi-square (pronounced "kai"). This test takes a two dimensional count table or cross-tabs and provides evidence for an association between the two variables.The test statistic comes from summing the deviations of the observed data has from expected values which represent the null hypothesis that there is no association. The computation for the expected cell values is represented by
The actual test statistic is computed by
The specific dataset I want is a 2x2 table of adult women who survived or did not, and their class.
I am going to test whether there was an association between the number of those that survived and passenger class for adult women. The following code will execute this test.
As you can see, the function to carry out this test is chisq.test. The p-value here is very small (p < 0.05) so I reject the null hypothesis and have sufficient evidence to claim there is an association between survival and passenger class for adult women aboard the Titanic.
Goodman & Kruskall's Gamma
Goodman and Kruskall's gamma is an elegant use of the additional information inherent in rank order data. This analysis is able to produce a test statistic analogous to Pearson's correlation coefficient for numeric (interval/ratio level) data. As a reminder, this is a statistic that ranges between -1 and 1, where -1 describes a perfect negative correlation, 1 describes a perfect positive correlation, and 0 describes no association. This analysis is particularly handy for surveys that use likert scales or other ordinal information.The association is estimated by comparing the diagonal elements of the ordinal levels to the off-diagonal elements. While I won't get into the details, I will illustrate this concept with tables that produce perfect positive and negative associations.
To make the application of this test more obvious, I created a fictitious table where one axis is education with ordinal categories and the other contains likert scale responses. Let's say that I am a public health official and I want to make an association with education and thoughts regarding immunizations. This survey has a number of questions, the first being one that asks about the respondents' level of education and the other is a question that asks "Please indicate how important you feel that immunizations are to your health and the health of your home town." After administering this survey to people in my area, I want to analyze those results in order to prove that association. The observed results provide the following cross-tabs.
The rows are the education levels and columns the responses to the question regarding immunizations. Without reading ahead, what kind of association do you see in this data based off of what you saw in the behavior of the perfect associations? Can you see a greater emphasis on the diagonal elements of the table?
The function for this gamma statistic can be found in two R packages, though I am sure there are more out there. The first being "DescTools" and the other being "vcdExtra". I like "vcdExtra" a bit more because it provides a confidence interval for the estimate.
The test statistic provides evidence for the association between education and sentiments regarding the importance of immunizations to public health.
That's a wrap for this post. Please let me know if you have any further questions, thoughts, or ideas in the comments. Lastly, feel free to ask me any specific questions at this site. Be aware that there is a nominal $1.50 fee to submit questions. That is because it takes time and effort to respond to your questions. Though, please ask questions about this specific post in the comments.
Comments
Post a Comment