Online Statistics Tutor: Introduction to Hypothesis Testing - Understanding and Interpreting Statistical Hypothesis Tests
Regardless of the statistical test that you are using, the process of rejecting or retaining a null hypothesis can be confusing for many. I'm not going to target any one hypothesis test, rather discuss the general logic.
My intention with this post is to provide students of introductory statistics courses (or anyone attempting to learn these concepts) some additional insight into how to understand and interpret hypothesis tests. Whether you are conducting a t-test, F-test, chi-square, or are testing regression coefficients from a model, the general idea behind it all is the same.
All statistical hypothesis tests follow the same general approach of testing the scenario of the null hypothesis. That is, there is no association or detectable effect with your outcome variable, also known as the dependent variable. The alternative hypothesis is usually the research hypothesis, e.g. soda affects obesity, or excessive exposure to business meetings is associated with reduced brain function. Whatever it is that you are trying to prove is your alternative hypothesis.
In a statistical hypothesis test, the "suspect" is your research hypothesis and the "trial" is the statistical test. You assume a state of innocence, which is the null hypothesis, unless proven guilty beyond a reasonable doubt. Being "guilty" is your alternative hypothesis and "beyond a reasonable doubt" or the burden of proof, is your confidence level. Each statistical hypothesis test is a separate trial for a given research hypothesis.
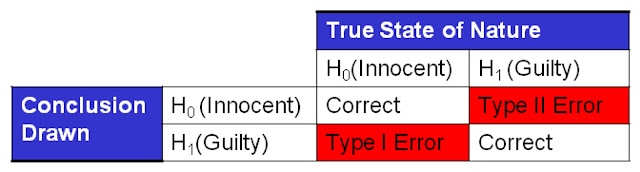
The outcomes of making a decision when confronted by these hypotheses is described in the table below.
There are 4 potential outcomes when you accept or reject the null hypothesis. Two are correct and two incorrect. The two errors involve letting a guilty person go free or prosecuting an innocent person. Both bad, but often you'd rather make one wrong decision versus the other. For example, the criminal justice system would rather let a guilty person go free, than imprison an innocent one. Hence, the burden of proof. Not that the criminal justice system doesn't make either wrong decision on occasion, just that they'd prefer a greater likelihood of letting guilty offenders go, as opposed to imprisoning innocent people.
Statistical hypothesis testing works in a very similar way (even if you are bayesian, your trial just looks a bit different). Statisticians and researchers would rather assume a true research hypothesis is false, than validate or "prove" a false hypothesis. 𝛂 or the type I error rate is your burden of proof in each trial or statistical test. Type II error or its opposite, 𝛃 often referred to as "power", describes the sensitivity of the statistical test in picking up "signal" in the data or evidence, if we follow the same analogy.
Let's put the decision dilemma problem in the context of a serious medical issue. For this example, we are testing a biopsy to see whether or not an individual has cancer. Scientific methods exist to see if a biopsy specimen is malignant or not. Of course, we always want to be right, but no test is infallible and if we are wrong, then which error would be more dire for the patient? Would it be worse to tell a healthy person that he/she has cancer, or worse to tell someone that has cancer that they are healthy? It would be MUCH worse to make a type II error in this case, because that puts that person's life in jeopardy, whereas a type I error would give a healthy person undue stress and anxiety for a time. Hopefully, this example helps you understand the need for and motivation behind burden of proof, or confidence level in testing various hypotheses.
All statistical tests assume a sampling distribution under the null hypothesis, and center around zero for symmetric sampling distributions. Non-symmetric sampling distributions such as those used in F-tests, and chi-square assume distributions under the null hypothesis, as well.
Having a test statistic greater than the critical value, or a p-value less than 𝜶 is the exact same thing. That is because the critical value is the point on null hypothesis sampling distribution where p = 𝜶. Specifically, the p-value represents the area underneath the curve beyond our test statistic. Which curve am I talking about? The sampling distribution of the test statistic assuming the null hypothesis is true. Let me show you visually what is going on and with the critical value and p-value. Keep in mind this will look much like what you already studied for z-scores and normal probability. That is because you are doing the same thing. See my post on normal probabilities if you need a refresher on that material.
The null hypothesis assumes no effect so the distribution is centered at 0. Many test statistics use normal / normal-like distributions (t-test, Wilk test for regression coefficients, etc.) and are divided by their standard error as part of the calculation which puts the end result on the scale of the standard normal distribution. The above graphic describes a two-tailed test so the critical value will have 2.5% of the area beyond that value at either end of the distribution. The area beneath the curve describes the likelihood of committing a type 1 error, so the smaller the area beyond our test statistic means we are less likely to commit that decision error. If the likelihood of a type I error is sufficiently low, then we reject the null hypothesis. An example may help clear up any confusion.
Let's say I have a test statistics, z = 0.6, and we are conducting a one-tailed test at 𝜶 = 0.05. As a reminder, to reject the null hypothesis we need our test statistic to be greater than the critical value or have p < 𝜶 (p less than alpha). For 𝜶 = 0.05, and a one-tailed test, our critical value will be z = 1.645 (use a z-table or stat software to find this) A test statistic of z = 0.6 corresponds to a p-value of 0.274.
Here we have our test statistic that is less than the critical value of 1.645, and equivalently, p > 𝜶 (p greater than alpha). This means that we should retain the null hypothesis that there is no significant effect. The burden of proof or alpha of 0.05 means we are willing to tolerate an estimated type I error rate of 5 out of 100 times. The p-value of 0.274 is saying that we have an estimated type I error rate 27.4 out of 100 times. This is much worse than the required level and must, consequently, retain the null hypothesis.
On the other hand, let's say we are performing a two-tailed test where, again 𝜶 = 0.05, and our test test statistic is z = 3.15.
In this next example, the test statistic (z = 3.15) is greater than the critical value of 1.96. Equivalently, p is less than alpha. The p-value of 0.0016 is telling us that given the test statistic of 3.15 we expect to commit a type I error 0.16 out of 100 times. That is much better than 5 out of 100 times, or 𝜶 = 0.05. With that, we should reject the null hypothesis and conclude that there IS a significant effect.
Hopefully, those example make it easier to understand when to accept or reject the null hypothesis, and what that looks like in terms of the sampling distribution of the test statistic under the null hypothesis.
I know this is dense material and a lot of it. However, I find that this material sticks better if we understand more about what is going on and why, rather than mechanically memorizing rules about p-values, test statistics, and critical values.
That is all the material for this online statistics tutor post. Feel free to request additional topics in the comments. Also, you are welcome to ask me specific questions that you may have regarding this material at this site. In the interest of full disclosure, there is a nominal $1.50 fee to submit questions. That is because it takes time and effort to respond to your questions. Thanks!
My intention with this post is to provide students of introductory statistics courses (or anyone attempting to learn these concepts) some additional insight into how to understand and interpret hypothesis tests. Whether you are conducting a t-test, F-test, chi-square, or are testing regression coefficients from a model, the general idea behind it all is the same.
All statistical hypothesis tests follow the same general approach of testing the scenario of the null hypothesis. That is, there is no association or detectable effect with your outcome variable, also known as the dependent variable. The alternative hypothesis is usually the research hypothesis, e.g. soda affects obesity, or excessive exposure to business meetings is associated with reduced brain function. Whatever it is that you are trying to prove is your alternative hypothesis.
Reasoning behind Hypothesis Testing
The idea behind this approach is similar to the decision dilemma the criminal justice system uses. In a criminal trial, a suspected offender is "innocent until proven guilty", right? The prosecution must provide evidence "beyond a reasonable doubt" that the accused committed the offense. If the prosecution isn't able to meet a certain level of certainty or confidence (a.k.a. burden of proof), then the suspect is assumed innocent of any wrong-doing.In a statistical hypothesis test, the "suspect" is your research hypothesis and the "trial" is the statistical test. You assume a state of innocence, which is the null hypothesis, unless proven guilty beyond a reasonable doubt. Being "guilty" is your alternative hypothesis and "beyond a reasonable doubt" or the burden of proof, is your confidence level. Each statistical hypothesis test is a separate trial for a given research hypothesis.
The outcomes of making a decision when confronted by these hypotheses is described in the table below.
There are 4 potential outcomes when you accept or reject the null hypothesis. Two are correct and two incorrect. The two errors involve letting a guilty person go free or prosecuting an innocent person. Both bad, but often you'd rather make one wrong decision versus the other. For example, the criminal justice system would rather let a guilty person go free, than imprison an innocent one. Hence, the burden of proof. Not that the criminal justice system doesn't make either wrong decision on occasion, just that they'd prefer a greater likelihood of letting guilty offenders go, as opposed to imprisoning innocent people.
Statistical hypothesis testing works in a very similar way (even if you are bayesian, your trial just looks a bit different). Statisticians and researchers would rather assume a true research hypothesis is false, than validate or "prove" a false hypothesis. 𝛂 or the type I error rate is your burden of proof in each trial or statistical test. Type II error or its opposite, 𝛃 often referred to as "power", describes the sensitivity of the statistical test in picking up "signal" in the data or evidence, if we follow the same analogy.
Let's put the decision dilemma problem in the context of a serious medical issue. For this example, we are testing a biopsy to see whether or not an individual has cancer. Scientific methods exist to see if a biopsy specimen is malignant or not. Of course, we always want to be right, but no test is infallible and if we are wrong, then which error would be more dire for the patient? Would it be worse to tell a healthy person that he/she has cancer, or worse to tell someone that has cancer that they are healthy? It would be MUCH worse to make a type II error in this case, because that puts that person's life in jeopardy, whereas a type I error would give a healthy person undue stress and anxiety for a time. Hopefully, this example helps you understand the need for and motivation behind burden of proof, or confidence level in testing various hypotheses.
Making a Decision and Interpretation of the Result
Odds are, your statistics course had you repeat phrases like "reject the null because there is sufficient evidence", or "retain the null because of insufficient evidence". Often there is confusion about when the p-value or test statistic indicate whether you should reject or retain the null hypothesis.All statistical tests assume a sampling distribution under the null hypothesis, and center around zero for symmetric sampling distributions. Non-symmetric sampling distributions such as those used in F-tests, and chi-square assume distributions under the null hypothesis, as well.
Having a test statistic greater than the critical value, or a p-value less than 𝜶 is the exact same thing. That is because the critical value is the point on null hypothesis sampling distribution where p = 𝜶. Specifically, the p-value represents the area underneath the curve beyond our test statistic. Which curve am I talking about? The sampling distribution of the test statistic assuming the null hypothesis is true. Let me show you visually what is going on and with the critical value and p-value. Keep in mind this will look much like what you already studied for z-scores and normal probability. That is because you are doing the same thing. See my post on normal probabilities if you need a refresher on that material.
Let's say I have a test statistics, z = 0.6, and we are conducting a one-tailed test at 𝜶 = 0.05. As a reminder, to reject the null hypothesis we need our test statistic to be greater than the critical value or have p < 𝜶 (p less than alpha). For 𝜶 = 0.05, and a one-tailed test, our critical value will be z = 1.645 (use a z-table or stat software to find this) A test statistic of z = 0.6 corresponds to a p-value of 0.274.
Here we have our test statistic that is less than the critical value of 1.645, and equivalently, p > 𝜶 (p greater than alpha). This means that we should retain the null hypothesis that there is no significant effect. The burden of proof or alpha of 0.05 means we are willing to tolerate an estimated type I error rate of 5 out of 100 times. The p-value of 0.274 is saying that we have an estimated type I error rate 27.4 out of 100 times. This is much worse than the required level and must, consequently, retain the null hypothesis.
On the other hand, let's say we are performing a two-tailed test where, again 𝜶 = 0.05, and our test test statistic is z = 3.15.
Hopefully, those example make it easier to understand when to accept or reject the null hypothesis, and what that looks like in terms of the sampling distribution of the test statistic under the null hypothesis.
I know this is dense material and a lot of it. However, I find that this material sticks better if we understand more about what is going on and why, rather than mechanically memorizing rules about p-values, test statistics, and critical values.
That is all the material for this online statistics tutor post. Feel free to request additional topics in the comments. Also, you are welcome to ask me specific questions that you may have regarding this material at this site. In the interest of full disclosure, there is a nominal $1.50 fee to submit questions. That is because it takes time and effort to respond to your questions. Thanks!
Comments
Post a Comment